Research – photonic structures

Introduction

Design of photonic structures allows tailoring a nearly unlimited variety of specific optical properties. For example, photonic crystals with defects can act as very narrow-band band-pass filters. With regards to the lack of natural materials with specific optical properties in the terahertz (THz) spectral region, fabrication of photonic structures is a promising mean of introducing the desired optical response. We particularly aim to the design of photonic structures controlled by external parameters such as electric field, illumination or temperature.

Our major achievements

Design of metamaterials for THz spectral region with negative permeability [1–3] and on-demand properties [4].
Studies of photonic structures for THz spectral region (photonic crystals, waveguides etc.) [5–9].
Development of ultrafast opto-terahertz modulators [10–12].
Conception and characterization of controllable THz photonic crystals [13–16].

Metamaterials for THz spectral region
Photonic crystals and their control by temperature
Ultrafast opto-terahertz modulators
Analysis of a segmented waveguide

Metamaterials for THz spectral region

Metamaterials are artificial structures composed of patterns with a high contrast of electromagnetic properties of constituent materials and with unit cell dimensions much smaller then the wavelength of the target spectral region. Since the incident light cannot resolve the patterns, the metamaterials behave as materials with some effective optical properties – we can assign them e.g. an effective permittivity and permeability or effective refractive index. By the design of suitable pattern, one can prepare metamaterials with optical properties not found in nature. In particular, there is a substantial interest in achieving negative refraction metamaterials which are characterized by simultaneously negative permittivity and permeability. Since negative permeability is seldom found at frequencies exceeding a few GHz, tailoring metamaterials is one of the few possibilities how to achieve negative permeability.

Negative effective permeability is frequently achieved in metallic split-ring resonators [IEEE Trans. Microwave Theory Tech. 47, 2075 (1999)]. Another approach takes advantage of strong localization of magnetic field inside dielectric rods with high permittivity when a Mie resonance is excited by an electromagnetic wave with electric polarization perpendicular to the rods [J. Phys.: Condens. Matter. 14, 4035 (2002)]. We have adopted the latter approach which allows us to control the resonant frequency by temperature tuning of the permittivity of dielectric rods [3]. Our structure is made of an incipient ferroelectric SrTiO₃ (Fig. 1a). The THz permittivity of SrTiO₃ is related mainly to the soft lattice vibration and it can be controlled by temperature. Decreasing the temperature leads to the increase of SrTiO₃ permittivity and thus to the decrease of the frequency of the Mie resonance, as can be seen in the transmittance spectra in Fig. 1b: the tuning range spans from 0.20 to 0.36 THz. Further on, we have measured transmittance and reflectance spectra of the metamaterial which allowed us to retrieve independently its effective permittivity and permeability and thus verify that the metamaterial exhibits a range of negative effective permeability (Fig. 1c). We have also shown that a broad range with negative effective permeability can be achieved by using rods with high aspect ratio [2].

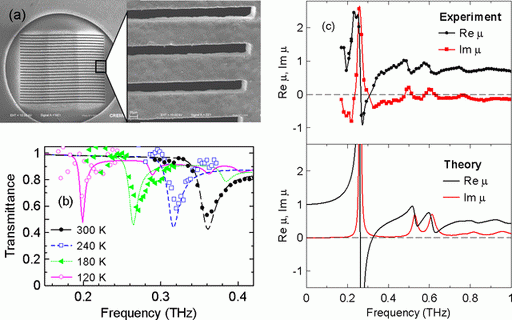
Fig. 1. (a) Scanning electron microscope image of the metamaterial. (b) Transmittance spectra of the metamaterial for various temperatures. The dip corresponds to the lowest Mie resonance which is associated with strong effective magnetic behavior. Points: measured spectra, lines: results of calculations by transfer-matrix method. (c) Effective magnetic permeability: real and imaginary of permeability (Re μ and Im μ, respectively) of the metamaterial. Top panel: measured spectra, bottom panel: results of calculations by transfer-matrix method. The structure in (c) has different geometrical parameters than in (a) and (b).

Etching an array of perpendicular micro-grooves into silicon wafers allows one to create an isotropic THz metamaterial with on-demand refractive index in the THz range [4]. Such a structure is shown in Fig. 2. In principle, the effective refractive index can be any value between the refractive index of air (n_air = 1) and of the wafer (n_Si = 3.4); in practice, this interval will be limited by the tiniest feature which can be created through the anisotropic etching. When grooves in one direction only are etched into the wafer, the resulting metamaterial becomes strongly anisotropic. We have demonstrated a structure which exhibits a birefringence of 1.2 [4].

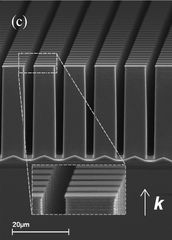
Fig. 2. Scanning electron microscope picture of the metamaterial with an isotropic on-demand refractive index. The structure consists of an array of square pillars formed by anisotropic etching of grooves in a silicon wafer.

Photonic crystals and their control by temperature

Photonic crystals are structures with periodic variation of refractive index (Fig. 3). They typically exhibit frequency regions (band gaps) in which the propagation of electromagnetic waves is forbidden. If their periodicity is broken (by substitution or by insertion of a defect layer etc.), extremely narrow defect modes appear in the forbidden bands; the corresponding transmission can easily reach 100 % (Fig. 4). The use of these structures for high-quality filtering in spectroscopy and in communication devices is thus a straightforward and potentially very promising application.

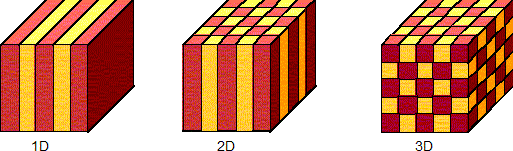
Fig. 3. Simple examples of photonic crystals with a one- to three-dimensional periodicity.

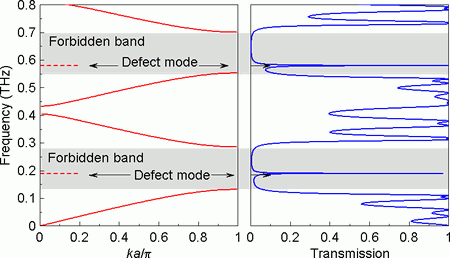
Fig. 4. Example of a band-structure of a one-dimensional photonic crystal composed of 6 lattice periods separated by a defect layer. The left panel shows its band-structure (a is the period length and k is a wave-vector); the right-panel contains its transmittance spectrum.

The wavelength corresponding to the first forbidden band is comparable to the optical thickness of one period. Photonic crystals for terahertz wavelengths (0.1 – 3 mm) thus require the use of a sub-millimetre lattice period, which makes the photonic crystals relatively easy to fabricate. Focus on the terahertz spectral region is the more important that basic optical elements (like spectral filters) operating in the terahertz region are still under development.

In order to extend the applicability of photonic crystals, it is desirable to find a means of their tunability. Currently, we are interested especially in one-dimensional photonic crystals. Their advantage is a great simplicity, which allows an analytical description of their properties [8, 9]. Consequently, it is possible to propose a photonic structure with desired properties and select appropriate constituting materials. Vice versa, it is also often straightforward to set up a design of photonic structures with desired properties. Among others, we have proposed widely tunable photonic-crystal-based filters [15, 16].

The investigated tunable filters consisted of a ferroelectric defect enclosed in a photonic crystal [15, 16]. For example, we used a SrTiO₃ crystal which exhibits a strong temperature dependence of dielectric permittivity: the permittivity changes by a factor of 7 when cooled from room temperature down to 75 K. Due to this pronounced temperature dependence we were able to construct a photonic crystal filter with tunability reaching 60 %. The scheme of the filter, its tuning curve and representative transmission spectra are shown in Fig. 5. It should be stressed out that the filter is all-solid and is thus only weakly susceptible to mechanical damage.

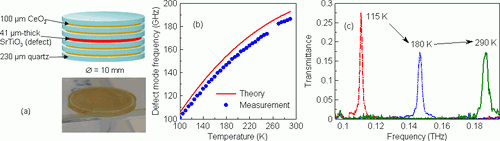
Fig. 5. (a) Structure of the investigated tunable photonic-crystal-based filter. The photography at the bottom shows the stack of the alternating layers of quartz and CeO₂ ceramics. (b) Tuning curve of the photonic crystal filter. Relative tunability reaching 60 % has been achieved. (c) Transmittance spectra of the photonic crystal filter measured at 115, 180 and 290 K.

Ultrafast opto-terahertz modulators

Terahertz technology is a research field which has a growing impact e.g. on medical, space and defence industries. As future short-range indoor communication systems may be designed for the sub-terahertz or terahertz range, one can expect a growing emphasis put on the manipulation of both guided and freely propagating terahertz beams by means of agile switches, modulators, and phase shifters controlled either optically or electronically. Optically controlled terahertz switches or filters are of particular interest as they are in principle able to achieve ultrahigh speeds.

High-resistivity semiconductors show a big potential for opto-terahertz coupling. In the ground state, they are transparent and dispersion free for terahertz radiation. Upon optical illumination, free carriers are generated: they exhibit a strong interaction with terahertz radiation, which can be tuned by the illumination. The semiconductor wafer then can be placed into a photonic structure in order to enhance the interaction and in order to achieve the THz modulation at low intensities of optical control pulses. In this case, the photonic structure can be designed in such a way that the terahertz electric field is spatially localized and enhanced in the photo-excited layer [10, 12]. Such a device is typically narrow-band, since the localization of the electromagnetic field occurs only at the defect-mode frequency. We have shown that the dynamical response is determined by the resonator lifetime (switch-on time) and by the photocarrier lifetime (switch-off time).

An example of the investigated photonic-crystal-based modulator is shown in Fig. 6. It consists of a sequence of alternating layers of quartz and MgO (materials with high contrast of refractive indices at terahertz wavelengths and with high transparency in the visible optical region are required). The device exhibits a response time of ~200 ps, making it possible to construct an opto-terahertz modulator with modulation rates up to 5 GHz.

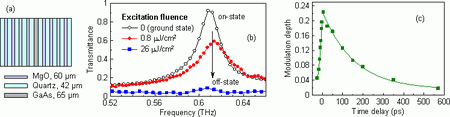
Fig. 6. (a) Scheme of the ultrafast photonic-crystal-based modulator. (b) Measured transmittance spectra for few excitation fluences. A modulation of 50 % can be achieved with excitation fluence as low as 0.8 µJ/cm². (c) Measured dynamical response of the opto-terahertz modulator at the defect-mode frequency (0.606 THz). The switch-on time is ~20 ps while the switch-off time is ~200 ps and it is limited by the photo-carrier lifetime.

Analysis of a segmented waveguide

Waveguiding structures with in-plane periodic pattern show very rich dispersion features, particularly for frequencies for which the Bragg diffraction condition is close to be satisfied. Such structures are important in integrated optics namely as stop-band filters, Bragg mirrors, input and output couplers and signal multiplexers or in nonlinear optics for achieving quasi-phase-matching condition for second harmonic generation. Performance of these elements can be considerably reduced by radiation losses encountered due to the periodicity of the structures. Understanding of the band structure and corresponding radiation losses is thus important for the design of efficient optical elements.

We have investigated both theoretically and experimentally a segmented waveguide made of silicon and designed for the terahertz spectral region [5]. For frequencies below 268 GHz, the structure exhibits only guided modes which do not couple to modes propagating in the exterior of the waveguide. For higher frequencies, the eigen-modes of the structure are leaky, i.e., they do radiate out of the waveguide and the electromagnetic energy in the waveguide decays upon guiding. Among others, we have employed a modal method which allows it to calculate the band structure of the guided and leaky modes and to calculate the radiation losses of leaky modes.

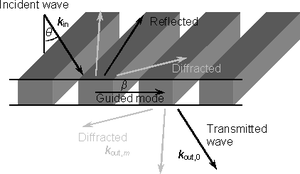
Fig. 7. Scheme of the investigated periodic segmented waveguide. The period was 385 µm, thickness 210 µm and volume filling factor 0.455. Such a waveguide exhibits leaky modes above 268 GHz.

Related publications

[1]	R. Yahiaoui, H. Němec, P. Kužel, F. Kadlec, C. Kadlec, and P. Mounaix, Tunable THz metamaterials based on an array of paraelectric SrTiO₃ rods, Appl. Phys. A 103, 689 (2011).
[2]	R. Yahiaoui, H. Němec, P. Kužel, F. Kadlec, C. Kadlec, and P. Mounaix, Broadband dielectric terahertz metamaterials with negative permeability, Opt. Lett. 34, 3541 (2009).
[3]	H. Němec, P. Kužel, F. Kadlec, C. Kadlec, R. Yahiaoui, and P. Mounaix, Tunable terahertz metamaterials with negative permeability, Phys. Rev. B 79, 241108 (2009).
[4]	C. Kadlec, F. Kadlec, P. Kužel, K. Blary, and P. Mounaix, Materials with on-demand refractive indices in the terahertz rang, Opt. Lett. 33, 2275 (2008).
[5]	H. Němec, P. Kužel, J.-L. Coutaz, and J. Čtyroký, Transmission properties and band structure of a segmented dielectric waveguide for the terahertz range, Opt. Commun. 273, 99 (2007).
[6]	V. Dvořák, and P. Kužel, Negative index of refraction in anisotropic nonmagnetic materials, Ferroelectrics 338, 195 (2006).
[7]	M. Schuster, N. Klein, P. Ruther, A. Trautmann, O. Paul, P. Kužel, and F. Kadlec, An interconnected 2D-TM EBG structure for millimeter and submillimeter waves, IEEE J. Selected Areas Commun. 23, 1378 (2005).
[8]	H. Němec, P. Kužel, F. Garet, and L. Duvillaret, Time-domain terahertz study of defect formation in one-dimensional photonic crystals, Appl. Opt. 43, 1965 (2004).
[9]	H. Němec, L. Duvillaret, F. Quemeneur, and P. Kužel, Defect modes caused by twinning in one-dimensional photonic crystals, J. Opt. Soc. Am. B 21, 548 (2004).
[10]	L. Fekete, F. Kadlec, H. Němec, and P. Kužel, Fast one-dimensional photonic crystal modulators for the terahertz range, Opt. Exp. 15, 8898 (2007).
[11]	L. Fekete, F. Kadlec, P. Kužel, and H. Němec, Ultrafast opto-terahertz photonic crystal modulator, Opt. Lett. 32, 680 (2007).
[12]	L. Fekete, J. Y. Hlinka, F. Kadlec, P. Kužel, and P. Mounaix, Active optical control of the terahertz reflectivity of high-resistivity semiconductors, Opt. Lett. 30, 1992 (2005).
[13]	P. Kužel and F. Kadlec, Tunable structures and modulators for THz light, Comptes Rendus Physique 9, 197 (2008).
[14]	P. Mounaix, E. Freysz, J. Degert, N. Daro, J.-F. Létard, P. Kužel, V. Vigneras, and L. Oyenhart, One-dimensional tunable photonic crystals with spin crossover material for the terahertz range, Appl. Phys. Lett. 89, 174105 (2006).
[15]	H. Němec, P. Kužel, L. Duvillaret, A. Pashkin, M. Dressel, and M. T. Sebastian, Highly tunable photonic crystal filter for the terahertz range, Opt. Lett. 30, 549 (2005).
[16]	H. Němec, L. Duvillaret, F. Garet, P. Kužel, P. Xavier, J. Richard, and D. Rauly, Thermally tunable filter for terahertz range based on a one-dimensional photonic crystal with a defect, J. Appl. Phys. 96, 4072 (2004).