Introduction

The Laboratory of Terahertz Spectroscopy in the Department of Dielectrics of the Institute of Physics in Prague was established during 1998 – 1999. Since then, the group has produced about 220 publications in impacted international journals.

The main tool of our research is the experimental technique called time-domain terahertz spectroscopy. This method is able to measure complex dielectric and conductivity spectra of various kinds of samples in a spectral range of 0.15 to 2.5 THz (5 to 85 cm⁻¹). We put the emphasis on the research of:

Ferroelectrics and related materials including namely investigation of the soft phonon mode dynamics in single crystals, ceramics and thin films in view of tunable THz applications
Photonic crystals, metamaterials and tunable elements for the terahertz range
Ultrafast photoconductivity in semiconductors and molecular systems (by means of time-resolved optical pump — terahertz probe experiments)
THz microscopy and near-field imaging.

Terahertz spectroscopy

The prefix Tera- denotes 10¹², or 1 000 000 000 000 (1 million million). One terahertz (1 THz) refers to an electromagnetic wave with 10¹² cycles per second, which corresponds to a vacuum wavelength of 0.3 mm. The frequency region arround 1 THz was frequently referred to as the “terahertz” gap dividing the electromagnetic spectrum to the world of electronics at lower frequencies and to the world of optics at higher frequencies (see Fig. 1). Indeed, the THz spectral range was difficult to access using both conventional optical methods and classical electronic transistor-based devices due to the absence of powerful sources.

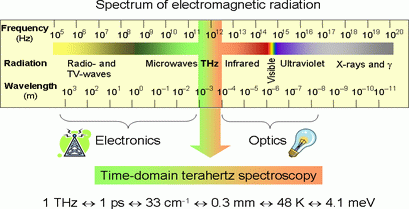
Fig. 1. Spectrum of electromagnetic radiation. Using time-domain terahertz spectroscopy, we are able to access the so-called terahertz (THz) gap.

A breakthrough came with the development of ultrafast lasers delivering femtosecond pulses in the optical spectral range (typically visible and near infrared). The so called optoelectronic approach to the generation and detection of broadband THz pulses makes use of the frequency conversion of optical pulses into the THz range. This technique, born at the beginning of 1990's, is called the time domain THz spectroscopy. The ultrashort laser pulses are converted in an emitter (which may be a non-linear crystal or a photoconductive antenna) into picosecond broadband pulses of terahertz radiation (Fig. 2). The technique involves a possibility of a phase-sensitive detection. To achieve this an element (again a nonlinear optical crystal or photoconductive antenna) sensitive to a simultaneous presence of the THz electric and optical pulse is used. The measured signal is proportional to the instantaneous value of the THz electric field overlapping with the “gating” femtosecond optical pulse. By scanning the time of arrival (delay) of the gating pulse, it is possible to reconstruct the temporal profile of the electric field of the terahertz pulse. Recent technological innovations in photonics and nanotechnology have lead to a dramatic increase in the interest of the scientific and industrial community in the THz research and applications.

Time-domain THz spectroscopy is able to measure complex dielectric and conductivity spectra of various kinds of samples in a spectral range typically of 0.1–5 THz. Its frequency spectrum can be calculated as its Fourier transformation. In addition, the use of laser pulses for the THz generation makes it possible to perform so called pump-probe experiments where the sample is first excited by an optical (UV, VIS, IR) pulse and, subsequently, it is probed by a delayed THz pulse. This technique allows one to access the far-infrared fingerprints of the ultrafast dynamics on sub-picosecond to nanosecond time scales. The THz waves are able to excite soft polar phonons in solids, vibrations of larger chains in biomolecules, to induce plasma oscillations of free charge carriers with concentrations of ~10¹⁴ – 10¹⁸ cm⁻³ and to interact with carriers localized in nanoparticles. It is then possible to investigate a broad range of physical systems and phenomena.

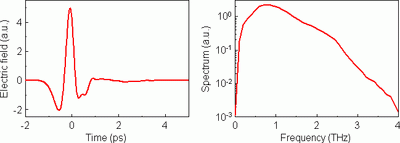
Fig. 2. An example of a temporal profile of electric field of a typical terahertz pulse (left panel) and its spectrum (right panel). The useful spectrum of the terahertz pulse spans over more than one decade (0.1 – 3 THz).

There are rich potential applications of the terahertz radiation:

Medical imaging: Terahertz radiation is able to penetrate up to several millimeters into some tissues with low water content. Its sensitivity to the water content makes it a promising probe of some type of cancers. Unlike X-rays, terahertz radiation is non-ionizing: its energy is too low to cause any damage to the tissue.
Security imaging: Terahertz radiation sees different things as compared to visible light. Notably, terahertz radiation passes through majority of plastics and clothes, but it does not penetrate through water. This makes the terahertz radiation an interesting tool for security checks.
Telecommunications: Systems based on waves with terahertz carrier frequencies can support a broadband modulation, and thus achieve very high transmission rates (principally of the order of 10¹¹ bits·s⁻¹).