Logo of the Laboratory of Terahertz in Prague Laboratory of Terahertz Spectroscopy, Prague
a group of Department of Dielectrics at Institute of Physics, v.v.i. 		Logo of the Institute of Physics

♦  Introduction
♦  Highlights
♦  Research topics
    –  Terahertz spectroscopy
    –  Ultrafast dynamics
    –  Ferroelectric materials
    –  Photonic structures
    –  Terahertz microscopy
    –  Medical application
♦  People
♦  Publications
♦  Equipment
♦  Collaborations
♦  Contact

Research – terahertz spectroscopy

Introduction

The time-domain terahertz (THz) spectroscopy is the main experimental tool of our research. It consists in the generation of picosecond broadband THz pulses, their interaction with the sample (in transmission or reflection geometry), and their phase sensitive detection. The detection is achieved by an optical sampling of the THz electric field profile (so called wave form) in the time domain. The Fourier transformation of the measured signal yields a complex THz spectrum E(f) which contains fingerprints of the dielectric (or possibly magnetic) behaviour of the sample. It is possible to retrieve the complex dielectric function or conductivity from the measured data in the range of about 0.1 to 3 THz.

This page summarizes our activities in the instrumentation and methodology of the time-domain terahertz spectroscopy.

Our major achievements

Contents

Generation and detection of terahertz pulses

We use two different schemes for the generation of THz pulses. The first one employs amplified laser pulses and makes use of an optical rectification (difference frequency mixing) in a nonlinear ZnTe crystal [A. Nahata et al., Appl. Phys. Lett., 69, 2321 (1996)]. This scheme is used namely for optical pump — THz probe experiments where amplified laser pulses are usually needed for optical excitation of the sample. The output THz pulses have a peak electric field attaining ~5 kV/cm, and a spectrum extending from about 0.2 to 2.5 THz. The second scheme is used with a femtosecond oscillator and takes advantage of a recently proposed high-brightness interdigitated semiconductor TeraSED photoswitch [A. Dreyhaupt et al., Appl. Phys. Lett. 86, 121114 (2005)]. Owing to its stability and reliability this method of generation is used for most standard steady-state (transmission) experiments. The electric field of the THz pulses attains ~100 V/cm, and the spectrum extends between 0.15 and 3 THz.

For phase-sensitive detection we use the electro-optic sampling scheme [A. Nahata et al., Appl. Phys. Lett., 69, 2321 (1996)]. A typical THz pulse and its spectrum generated and detected by a pair of [110]-cut 1 mm thick ZnTe crystals is shown in Fig. 1. A photo of our home-made THz spectrometer is shown in Fig. 2.


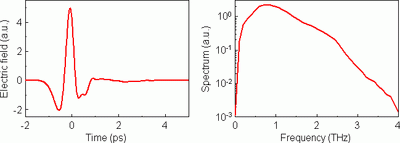
Fig. 1. Left panel: Example of the waveform measured in the transmission setup from Fig. 3. Right panel: Spectrum (Fourier transformation) of this waveform.


Fig. 2. Photo of our THz spectrometer. (1) THz emitter, (2) THz beam, (3) sample (in a flow cuvette), (4) optical pump pulse (not used in steady-state experiments), (5) Transmitted THz beam directed towards the detection, (6) gating optical pulse of electro-optic detection, (7) electro-optic sensor, (8) vacuum chamber.

Time-domain terahertz transmission spectroscopy (TDTTS)

Principle of the method. TDTTS is a recently introduced and now well established method of materials science. It covers a broad frequency range extending from tens of GHz up to few THz thus bridging a large gap between microwave and conventional infrared spectroscopies. Moreover, as a phase-sensitive method, TDTTS provides a direct access to both real and imaginary part of the dielectric function of the studied material with no need to perform the Kramers-Kronig analysis and with no a priori fitting model.


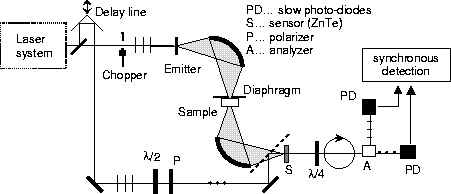
Fig. 3. Experimental scheme for time-domain terahertz transmission spectroscopy.

The technique (see Fig. 3) requires to measure the temporal profile of the electric field of a terahertz (THz) pulse transmitted through the investigated sample [8]. This is done by scanning the position of the delay line, which corresponds to the time delay between the THz pulse and the sampling beam. An example of a waveform obtained in this way is shown in Fig. 1. The complex spectrum of this pulse is divided by a reference spectrum (obtained when the sample is removed from the THz beam) yielding thus a frequency dependent complex transmission function of the sample. Finally, the complex refractive index N in the whole studied frequency range is obtained through a numerical solution of the system of two real nonlinear equations for the complex transmission function t:

t=4N/(N+1)^2 exp[i omega (N-1) d / c] sum_{k=0}^m [(N-1)/(N+1) exp(i omega N d / c)]^(2k) (1)

where d is the sample thickness, c is the speed of light and m is the number of internal (Fabry-Pérot) reflections in the sample. If these reflections are experimentally resolved (for thick samples) they form separate pulses in the measured signal so that the value of the coefficient m can be easily determined; for thin samples the Fabry-Pérot reflections overlap in time and the geometrical series should be summed up to the infinity.

The frequency resolution of the measurements is related to the length of the temporal scan T via the Nyquist criterion Δω = 2π/T. The upper and lower frequency limits are given by the properties of the THz emitter and receiver.

Time-domain terahertz reflection spectroscopy (TDTRS)

While the transmission setup has become a more or less routine method, it can only be applied to samples which are transparent in the THz region. However, one cannot always obtain sufficiently thin samples of materials with a high absorption coefficient. In that case, one needs to consider detecting the reflected beam instead of the transmitted one. As in the case of the transmission setup, it is necessary to measure a reference spectrum, in this case a spectrum of the beam reflected by a known substance (preferably a metal surface). With conventional approaches, the method had a principal difficulty which restricted or even hindered a precise evaluation of the data. Namely, it was necessary to ensure that the position and angle of the sample be exactly the same as that of the reference material (with a high precision, better than 1 µm). If this condition was not fulfilled, it was not possible to measure correctly the reflectivity phase, because the misplacement added an error to the phase shift.

We have developed a method [6] which enables measuring the THz reflectance of films and bulk samples with a phase sensitivity and circumvents the need of precise sample positioning. The idea is to let not only the THz, but also the sampling beam reflect off the sample and reference surface (see Fig. 4). Then, even a relatively big shift of the reflecting surface changes both optical paths in the same way, which has virtually no influence on the measured waveform and the optical constants can be evaluated precisely. This novel approach opens the way to measurements of many materials of high interest for materials science, especially of opaque materials and high permittivity dielectric thin films.


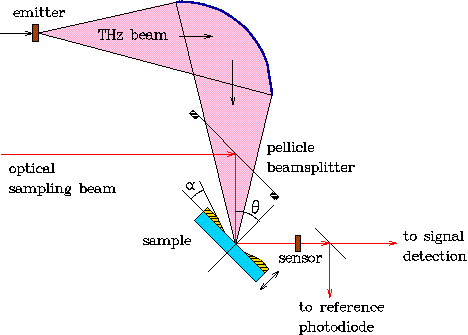
Fig. 4. Principle of reflectivity measurements with phase sensitivity. Both the THz and the sampling beam reflect off the sample, so that the sample / reference positioning need not be absolutely precise.

Time-domain terahertz emission spectroscopy (TDTES)

Information about sub-ps dynamics of photo-excited carriers in ultrafast semiconductors can be extracted from the temporal waveform of the THz pulses which are emitted from biased samples. The advantage of this method is that, contrarily to the all-optical pump-probe time-resolved reflectivity experiments, (i) the photo-induced absorption is avoided, (ii) the measurement is not sensitive to the carrier cooling, and (iii) that low carrier densities (less than 1015 cm−3) are used: thus the trap filling and the screening of the carriers can be completely neglected. On the other hand, the time resolution is decreased, nevertheless, time constants as small as 250 fs can be detected. The emitted THz signal is detected in the far field through electro-optic (EO) sampling (Fig. 5). This far-field profile is proportional to the time derivative of the current between the electrodes. It is important to stress that no focusing optics should be used in the path of the THz beam in order to avoid the waveform distortion due to the phase change and spectral filtering [9]. The detector response has to be carefully evaluated and taken into account [7]; this procedure seems to be simpler for electro-optic sampling than for antenna receivers. The complex THz spectrum is in this case simply multiplied by the autocorrelation of the optical pulse and by spectral characteristics of the electro-optic crystal.


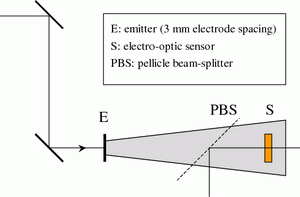
Fig. 5.Experimental setup for time-domain terahertz emission spectroscopy.

Rectification at metal surfaces

Recently, we have demonstrated a new possibility of generating pulsed THz radiation by means of optical rectification at metal surfaces [4, 5]. This phenomenon is due to an effective second-order non-linear susceptibility tensor χijk which vanishes in the bulk of the (centrosymmetric) metals, but is non-zero at the surface and just below due to the absence of translational symmetry. This has been known for decades, as second-harmonic generation at metal surface is well-known. By contrast, optical rectification at metals was not observed until recently. With amplified pulses, we were able to achieve a peak intensity of the electrical field of 4 kV/cm, comparable to that obtained with non-linear crystals. Further research on the topic is in progress.

Independent determination of dielectric and magnetic properties

In most cases, the THz spectroscopy is applied to the characterization of dielectric properties. In non-magnetic media, it is then a matter of taste whether we determine the refractive index N or the (relative) permittivity ε since &epsilon =N2. The situation is more complicated in media exhibiting both dielectric and magnetic response: they are now characterized by a dielectric permittivity ε and by a (relative) magnetic permeability μ, (both are complex quantities, generally frequency-dependent). The essential optical properties are now the refractive index N and the wave-impedance Z which are defined as

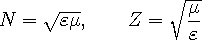N=sqrt(εμ), Z=sqrt(μ/ε) (2)

The refractive index N describes the propagation of electromagnetic waves in the bulk, while the wave-impedance Z determines the reflection losses at interfaces between media.

In contrast to common dielectric-only measurements, characterization of magnetic materials consists in the determination of two complex quantities (ε and μ, or equivalently, N and Z). In turn, two independent (complex) spectroscopic quantities have to be measured. A straightforward approach applicable for continuous THz radiation was developed by Smith et al. [Phys. Rev. B 65, 19 5104 (2002)]; it requires the knowledge of complex transmittance and reflectance spectra of the investigated sample.

Here we take advantage of the properties of time-domain THz spectroscopy: this method offers the possibility of the time windowing of the measured signal, i.e. one can identify and separate distinct pulses in the time-domain signal wave form, which correspond to internal reflections in the sample. In turn, one can measure transmittance and/or reflectance spectra corresponding to any pair of these reflections, and extract N and Z from these data [2]. These methods were validated upon characterization of non-magnetic samples. For example, Fig. 6 shows the dielectric and magnetic properties of a sapphire plate retrieved from transmittance spectra corresponding to the direct pass and to the first internal reflection of the THz pulse. The refractive index can be determined with an excellent precision, while much lower accuracy is encountered in the determination of the wave impedance. This is due to the fact that the refractive index leaves its fingerprints in the transmittance spectra during the propagation through the entire sample while the wave-impedance plays role only upon the two reflections at the sample surfaces. Such a behavior is characteristic for all extraction methods.


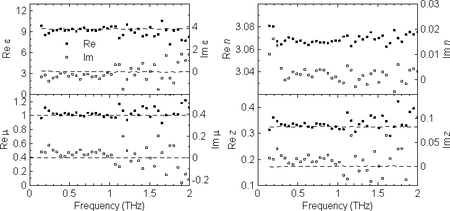
Fig. 6. Independently determined spectra of ε, μ, N, and Z of a sapphire plate.

Gouy shift correction

The accuracy of the determination of the complex refractive index essentially depends on the precision of the sample thickness determination, provided the model of the transmission function used for the retrieval is correct. However, the standard routine for the retrieval of the sample refractive index based on Eq. 1 assumes plane-wave approximation while the terahertz spectroscopic measurements are usually performed in focused beam geometry. The tight focusing is a frequent issue in the THz spectroscopy as the typical dimensions of the samples exceed the sub-THz wavelengths only by a factor smaller than 10. It is well-known that spatially limited ultrashort THz pulses change their phase dramatically (so called Gouy phase shift) close to their focus [9]. It follows that further improvements of the accuracy of THz spectroscopy must take into account the spatial properties of the THz beam. We proposed such a model for the transmission function which accounts for spatially limited Gaussian terahertz beams.

We assume that the sample is placed close to a focal plane in between two focusing elements (mirrors, lenses) similarly as in Fig. 7. Introduction of a homogeneous sample with thickness d and refractive index n displaces the focus position by Δ = d(n − 1)/n in the z direction (note that in general n may be a frequency-dependent quantity and, consequently, the shift may slightly vary with frequency). The focus position at the sensor is then displaced, too, by a distance Δ′. This causes an additional phase shift φ of the measured wave. Within the Gaussian beam approximation and as Δ′ is usually small, we obtain:

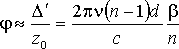φ ≈ Δ′/z_0 = 2πν(n-1)d/c β/n (3)

where z0 is the confocal parameter and the dimensionless frequency-dependent parameter β depends on the beam-waist size in the focus (which is also frequency dependent) and it is characteristic for a given experimental setup, typically of the order of 10−2 – 10−3. The highest values of β are found at low frequences (below 1 THz) and they decrease at higher frequencies.

One can show that the plane-wave approximation overestimates the true value n of the refractive index of a sample. The Gouy shift correction of the refractive index is of the order of β:

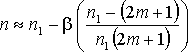n ≈ n_1 – β ((n_1–(2m+1))/(n_1(2m+1))) (4)

where m denotes the m-th Fabry-Pérot echo of the THz signal (m = 0 stands for the direct pass) and n1 is the value retrieved from the experimental data within the plane-wave approximation. The correction term is thus different for each echo, namely it changes the sign for higher order echoes. It follows that the Gouy shift has also an influence on the sample thickness determination from several echoes of time-windowed signal. This method relies on the fact that the total thickness of the medium probed by m-th echo varies with the echo number m: (2m + 1)d [see L. Duvillaret, F. Garet, and J.-L. Coutaz, Appl. Opt. 38, 409 (1999)] . The retrieved refractive index then depends on the echo number if a wrong thickness of the sample is used in the retrieval procedure. Our findings show that this method needs to be revisited, too, if a high precision of the thickness determination is required. This is the case, e.g. of the spectroscopy of very thin films on thick substrates.


Fig. 7. Scheme of an experimental setup containing 3 focal planes (for an emitter, sample and sensor). The displacement Δ of an object plane yields a displacement Δ′ of its image. The arrows indicate the shifts of foci.


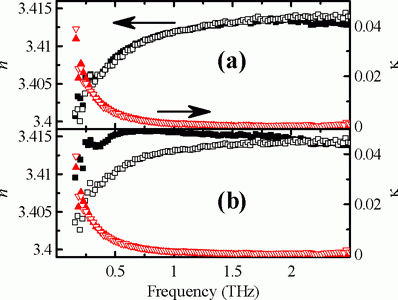
Fig. 8. Refractive index of a 1.933 mm thick Si wafer calculated from the direct pass (closed symbols) and from the first echo (open symbols). Retrieval by using (a) Gaussian beam approximation and (b) plane wave approximation.

Related publications

[1]P. Kužel, H. Nìmec, F. Kadlec, and C. Kadlec, Gouy shift correction for highly accurate refractive index retrieval in time-domain terahertz spectroscopy, Opt. Exp. 18, 15338 (2010). PDF file
[2]H. Nìmec, F. Kadlec, P. Kužel, L. Duvillaret, and J.-L. Coutaz, Independent determination of the complex refractive index and wave impedance by time-domain terahertz spectroscopy, Opt. Commun. 260, 175 (2006). Private PDF file
[3]H. Nìmec, C. Kadlec, F. Kadlec, P. Kužel, R. Yahiaoui, U-C. Chung, C. Elissalde, M. Maglione, and P. Mounaix, Resonant magnetic response of TiO2 microspheres at terahertz frequencies, Appl. Phys. Lett. 100, 061117 (2012). PDF file
[4]F. Kadlec, P. Kužel, J.-L. Coutaz, Study of terahertz radiation generated by optical rectification on thin gold films, Opt. Lett. 30, 1402 (2005). Private PDF file
[5]F. Kadlec, P. Kužel, and J.-L. Coutaz, Optical rectification at metal surfaces, Opt. Lett. 29, 2674 (2004). Private PDF file
[6]A. Pashkin, M. Kempa, H. Nìmec, F. Kadlec, and P. Kužel, Phase-sensitive time-domain terahertz reflection spectroscopy, Rev. Sci. Instrum. 74, 4711 (2003). PDF file
[7]H. Nìmec, A. Pashkin, P. Kužel, M. Khazan, S. Schnüll, and I. Wilke, Carrier dynamics in low-temperature grown GaAs studied by terahertz emission spectroscopy, J. Appl. Phys. 90, 1303 (2001). PDF file
[8]P. Kužel, and J. Petzelt, Time-resolved terahertz transmission spectroscopy of dielectrics, Ferroelectrics 239, 949 (2000). Private PDF file
[9]P. Kužel, M. A. Khazan, and J. Kroupa, Spatiotemporal transformations of ultrashort terahertz pulses, J. Opt. Soc. Am. B 16, 1795 (1999). Private PDF file
last change December 13, 2018 (home page)